nlcpy.logspace

nlcpy.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None, axis=0)[source]

Returns numbers spaced evenly on a log scale.

In linear space, the sequence starts at base ** start (base to the power of start) and ends with base ** stop (see endpoint below).

Parameters

startarray_like: base ** start is the starting value of the sequence.
stoparray_like: base ** stop is the final value of the sequence, unless endpoint is False. In that case, num + 1 values are spaced over the interval in log-space, of which all but the last (a sequence of length num) are returned.
numint, optional: Number of samples to generate. Default is 50.
endpointbool, optional: If true, stop is the last sample. Otherwise, it is not included. Default is True.
basefloat, optional: The base of the log space. The step size between the elements in ln(samples) / ln(base) (or log_base(samples)) is uniform. Default is 10.0.
dtypedtype, optional: The type of the output array. If dtype is not given, infer the data type from the other input arguments.
axisint, optional: The axis in the result to store the samples. Relevant only if start or stop are array-like. By default (0), the samples will be along a new axis inserted at the beginning. Use -1 to get an axis at the end.

Returns

samplesndarray: num samples, equally spaced on a log scale.

See also

arange: Returns evenly spaced values within a given interval.
linspace: Returns evenly spaced numbers over a specified interval.

Note

Logspace is equivalent to the code

>>> import nlcpy as vp
>>> y = vp.linspace(start, stop, num=num, endpoint=endpoint)
...  
>>> vp.power(base, y).astype(dtype)
...  

Examples

>>> import nlcpy as vp
>>> vp.logspace(2.0, 3.0, num=4)  
array([ 100.        ,  215.443469  ,  464.15888336, 1000.        ])
>>> vp.logspace(2.0, 3.0, num=4, endpoint=False) 
array([100.        , 177.827941  , 316.22776602, 562.34132519])
>>> vp.logspace(2.0, 3.0, num=4, base=2.0) 
array([4.        , 5.0396842 , 6.34960421, 8.        ])

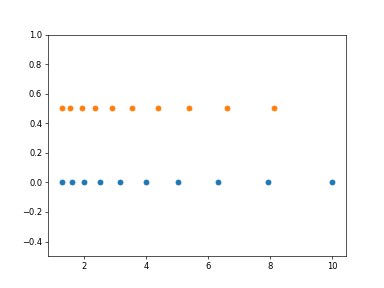
Graphical illustration:

>>> import matplotlib.pyplot as plt
>>> N = 10
>>> x1 = vp.logspace(0.1, 1, N, endpoint=True)
>>> x2 = vp.logspace(0.1, 1, N, endpoint=False)
>>> y = vp.zeros(N)
>>> plt.plot(x1, y, 'o') 
>>> plt.plot(x2, y + 0.5, 'o') 
>>> plt.ylim([-0.5, 1])
(-0.5, 1.0)
>>> plt.show()