nlcpy.random.Generator.lognormal

Generator.lognormal(self, mean=0.0, sigma=1.0, size=None)

Draws samples from a log-normal distribution.

Draws samples from a log-normal distribution with specified mean, standard deviation, and array shape. Note that the mean and standard deviation are not the values for the distribution itself, but of the underlying normal distribution it is derived from.

Parameters

meanfloat, optional: Mean value of the underlying normal distribution. Default is 0.
sigmafloat, optional: Standard deviation of the underlying normal distribution. Must be non-negative. Default is 1.
sizeint or tuple of ints, optional: Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn.

Returns

outndarray: Drawn samples from the parameterized log-normal distribution.

Note

A variable x has a log-normal distribution if log(x) is normally distributed. The probability density function for the log-normal distribution is:

$p(x) = \frac{1}{\sigma x \sqrt{2\pi}}e^{(-\frac{(ln(x)-\mu)^2}{2\sigma^2})}$

where $\mu$ is the mean and $\sigma$ is the standard deviation of the normally distributed logarithm of the variable.

Restriction

If mean is neither a scalar nor None : NotImplementedError occurs.
If sigma is neither a scalar nor None : NotImplementedError occurs.

Examples

Draw samples from the distribution:

>>> import nlcpy as vp
>>> rng = vp.random.default_rng()
>>> mu, sigma = 3., 1. # mean and standard deviation
>>> s = rng.lognormal(mu, sigma, 1000)

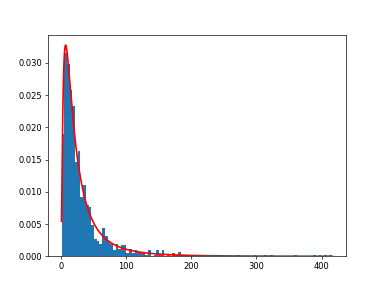
Display the histogram of the samples, along with the probability density function:

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s.get(), 100, density=True, align='mid')

>>> x = vp.linspace(min(bins), max(bins), 10000)
>>> pdf = (vp.exp(-(vp.log(x) - mu)**2 / (2 * sigma**2))
...        / (x * sigma * vp.sqrt(2 * vp.pi)))

>>> plt.plot(x, pdf, linewidth=2, color='r') 
... 
>>> plt.axis('tight') 
>>> plt.show()

../../_images/nlcpy-random-Generator-lognormal-1.png