nlcpy.random.Generator.standard_cauchy

Generator.standard_cauchy(self, size=None)

Draws samples from a standard Cauchy distribution with mode = 0.

Also known as the Lorentz distribution.

Parameters

sizeint or tuple of ints, optional: Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn.

Returns

samplesndarray: The drawn samples.

Note

The probability density function for the full Cauchy distribution is

$P(x; x_0, \gamma) = \frac{1}{\pi \gamma \bigl[ 1+(\frac{x-x_0}{\gamma})^2 \bigr] }$

and the Standard Cauchy distribution just sets $x_0=0$ and $\gamma = 1$

Examples

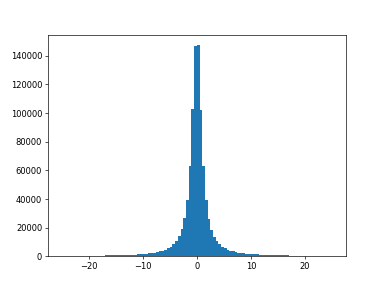
Draw samples and plot the distribution:

>>> import nlcpy as vp
>>> import matplotlib.pyplot as plt
>>> s = vp.random.default_rng().standard_cauchy(1000000)
>>> s = s[(s>-25) & (s<25)]  # truncate distribution so it plots well
>>> plt.hist(s.get(), bins=100) 
>>> plt.show()

../../_images/nlcpy-random-Generator-standard_cauchy-1.png