nlcpy.random.RandomState.normal

RandomState.normal(self, loc=0.0, scale=1.0, size=None)

Draws random samples from a normal (Gaussian) distribution.

The probability density function of the normal distribution, first derived by De Moivre and 200 years later by both Gauss and Laplace independently, is often called the bell curve because of its characteristic shape (see the example below). The normal distributions occurs often in nature. For example, it describes the commonly occurring distribution of samples influenced by a large number of tiny, random disturbances, each with its own unique distribution.

Parameters

locfloat: Mean (“centre”) of the distribution.
scalefloat: Standard deviation (spread or “width”) of the distribution. Must be non-negative.
sizeint or tuple of ints, optional: Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn.

Returns

outndarray: Drawn samples from the parameterized normal distribution.

Note

The probability density for the Gaussian distribution is

$p(x) = \frac{1}{\sqrt{ 2 \pi \sigma^2 }} e^{ - \frac{ (x - \mu)^2 } {2 \sigma^2}},$

where $\mu$ is the mean and $\sigma$ the standard deviation. The square of the standard deviation, $\sigma^2$ , is called the variance.

The function has its peak at the mean, and its “spread” increases with the standard deviation (the function reaches 0.607 times its maximum at nlcpy.random.normal is more likely to return samples lying close to the mean, rather than those far away.

Restriction

If loc is neither a scalar nor None : NotImplementedError occurs.
If scale is neither a scalar nor None : NotImplementedError occurs.

Examples

Draw samples from the distribution:

>>> import nlcpy as vp
>>> mu, sigma = 0, 0.1 # mean and standard deviation
>>> s = vp.random.normal(mu, sigma, 1000)

Verify the mean and the variance:

>>> abs(mu - vp.mean(s)) 
array(0.00206415)  # may vary
>>> abs(sigma - vp.std(s, ddof=1)) 
array(0.00133596)  # may vary

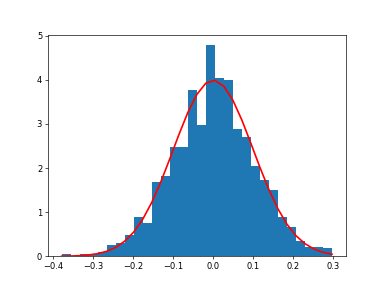
Display the histogram of the samples, along with the probability density function:

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s.get(), 30, density=True)
>>> plt.plot(bins, 1/(sigma * vp.sqrt(2 * vp.pi)) *
...          vp.exp( - (bins - mu)**2 / (2 * sigma**2) ),
...          linewidth=2, color='r') 
>>> plt.show()

../../_images/nlcpy-random-RandomState-normal-1_00_00.png

Two-by-four array of samples from N(3, 6.25):

>>> vp.random.normal(3, 2.5, size=(2, 4))    
array([[-4.49401501,  4.00950034, -1.81814867,  7.29718677],   # random
       [ 0.39924804,  4.68456316,  4.99394529,  4.84057254]])  # random