nlcpy.random.RandomState.random_integers

RandomState.random_integers(self, low, high=None, size=None)

Random integers of type nlcpy.int64/nlcpy.int32 between low and high, inclusive.

Return random integers of type nlcpy.int64/nlcpy.int32 from the “discrete uniform” distribution in the closed interval [low, high]. If high is None (the default), then results are from [1, low].

Parameters

lowint

Lowest (signed) integer to be drawn from the distribution (unless high=None, in which case this parameter is the highest such integer).

highint, optional

If provided, the largest (signed) integer to be drawn from the distribution (see above for behavior if high=None).

sizeint or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn.

Returns

outndarray of ints

size-shaped array of random integers from the appropriate distribution.

See also

RandomState.randint

Returns random integers from low (inclusive) to high (exclusive).

Note

To sample from N evenly spaced floating-point numbers between a and b, use:

a + (b - a) * (vp.random.random_integers(N) - 1) / (N - 1.)

Examples

>>> import nlcpy as vp
>>> vp.random.random_integers(5)    
array(2) # random
>>> type(vp.random.random_integers(5))
<class 'nlcpy.core.core.ndarray'>
>>> vp.random.random_integers(5, size=(3,2))  
array([[5, 4], # random
       [3, 3],
       [4, 5]])

Choose five random numbers from the set of five evenly-spaced numbers between 0 and 2.5, inclusive (i.e., from the set {0, 5/8, 10/8, 15/8, 20/8}):

>>> 2.5 * (vp.random.random_integers(5, size=(5,)) - 1) / 4. 
array([ 0.625,  1.25 ,  0.625,  0.625,  2.5  ]) # random

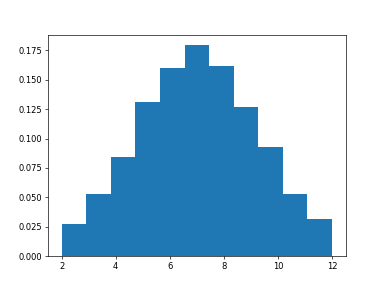
Roll two six sided dice 1000 times and sum the results:

>>> d1 = vp.random.random_integers(1, 6, 1000)
>>> d2 = vp.random.random_integers(1, 6, 1000)
>>> dsums = d1 + d2

Display results as a histogram:

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(dsums.get(), 11, density=True)
>>> plt.show()