nlcpy.random.RandomState.weibull

RandomState.weibull(self, a, size=None)

Draws samples from a Weibull distribution.

Draws samples from a 1-parameter Weibull distribution with the given shape parameter a.

$X = (-ln(U))^{1/a}$

Here, U is drawn from the uniform distribution over (0,1]. The more common 2-parameter Weibull, including a scale parameter $\lambda$ is just

$X = \lambda(-ln(U))^{1/a}$

Parameters

afloat: Shape parameter of the distribution. Must be nonnegative.
sizeint or tuple of ints, optional: Output shape. If the given shape is, e.g., (m, n, k), then m * n * k samples are drawn.

Returns

outndarray: Drawn samples from the parameterized Weibull distribution.

See also

RandomState.gumbel: Draws samples from a Gumbel distribution.

Note

The probability density for the Weibull distribution is

$p(x) = \frac{a}{\lambda}(\frac{x}{\lambda})^{a-1} e^{-(x/\lambda)^a},$

where $a$ is the shape and $\lambda$ the scale.

The function has its peak (the mode) at $\lambda(\frac{a-1}{a})^{1/a}$ .

When a = 1, the Weibull distribution reduces to the exponential distribution.

Restriction

If a is neither a scalar nor None : NotImplementedError occurs.

Examples

Draw samples from the distribution:

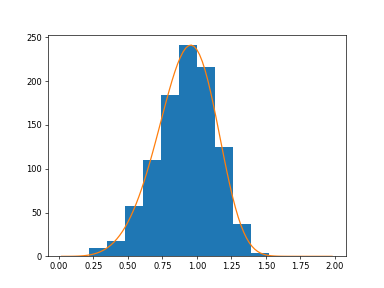
>>> import nlcpy as vp
>>> a = 5. # shape
>>> s = vp.random.weibull(a, 1000)

Display the histogram of the samples, along with the probability density function:

>>> import matplotlib.pyplot as plt
>>> x = vp.arange(1,100.)/50.
>>> def weib(x,n,a):
...     return (a / n) * (x / n)**(a - 1) * vp.exp(-(x / n)**a)

>>> count, bins, ignored = plt.hist(s.get())
>>> x = vp.arange(1,100.)/50.
>>> scale = count.max()/weib(x, 1., 5.).max()
>>> plt.plot(x, weib(x, 1., 5.)*scale) 
>>> plt.show()

../../_images/nlcpy-random-RandomState-weibull-1.png