Example: Thermal Simulation (Naive Implementation)

Objective
Physics
Program
Simulation Result

Objective 

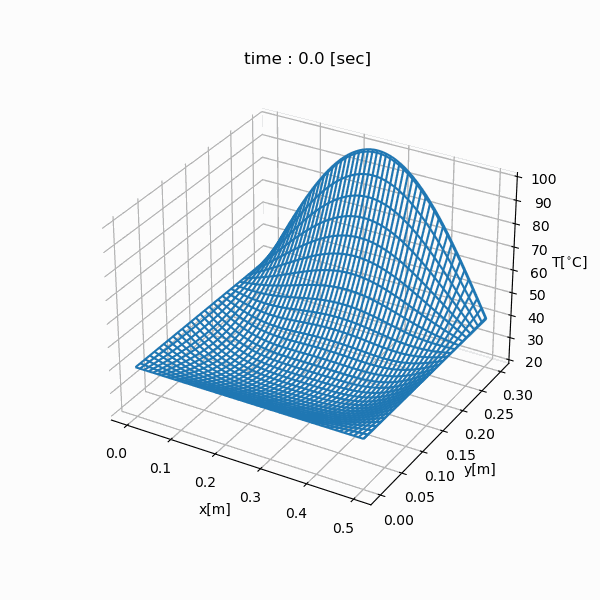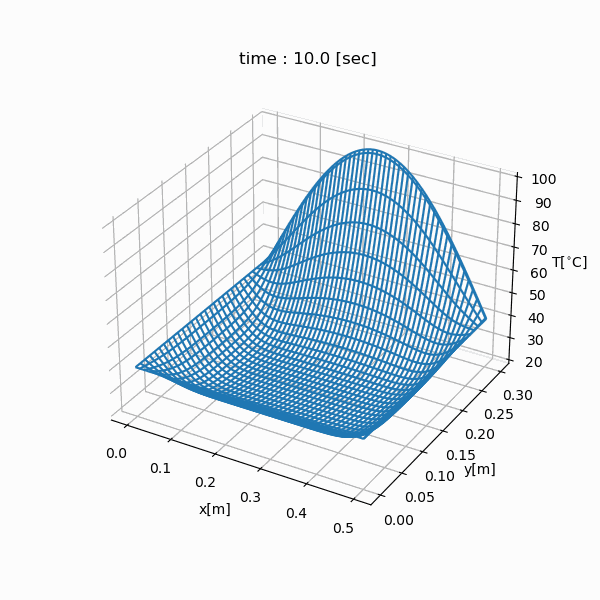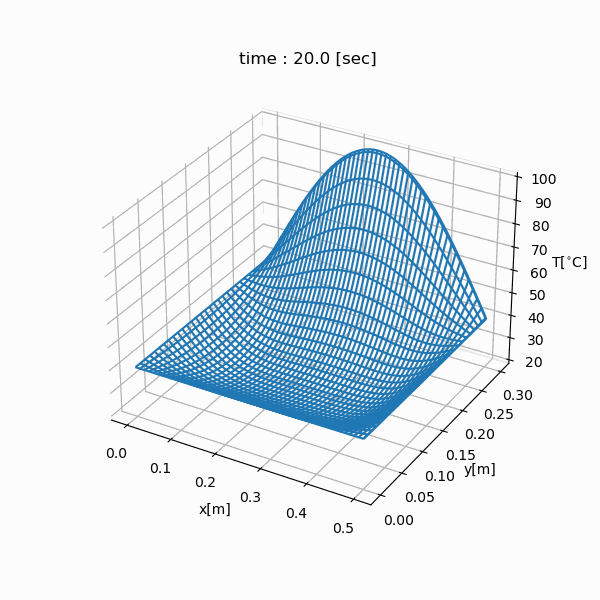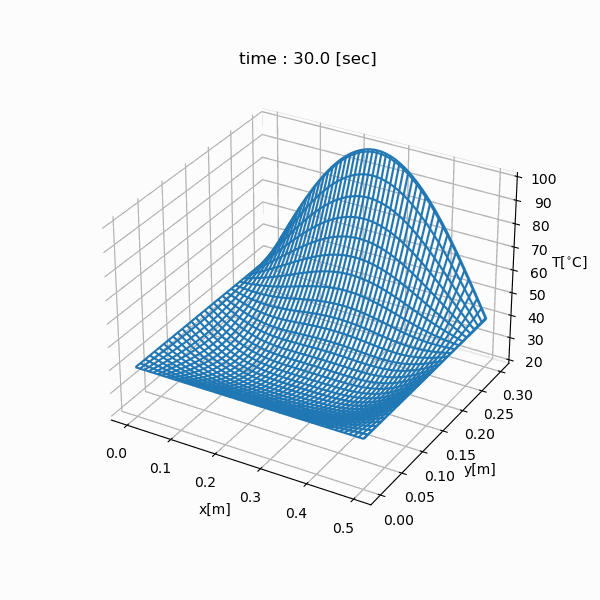
We will simulate the temporal change in temperature of the copper rectangle whose length is 50 cm (= LX), width is 30 cm (= LY) using a finite-difference method.

Physics 

Governing Equation 

$\frac{\partial}{\partial t} T=\frac{k}{\rho c}\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right)T$

Variable	Description
$T$	Temperature [K]
$t$	Time [s]
$x$	x coordinate [m]
$y$	y coordinate [m]

Constant	Description	Value of Copper
$k$	Thermal conductivity	398.0 [W/m K]
$\rho$	Density	8960.0 [kg/m ³]
$c$	Specific heat capacity	385.0 [J/kg K]

Boundary Conditions 

$\begin{eqnarray*} T &=& T_1 ~ (x=0, x={\rm LX}, y=0) \\ T &=& T_1+T_2 \sin \frac{\pi x}{\mathrm LX} ~ (y={\rm LY}) \\ \end{eqnarray*}$

Initial Conditions 

$\begin{eqnarray*} T &=& T_0 \\ \end{eqnarray*}$

Program 

import nlcpy as vp
from matplotlib import pyplot as plt
from matplotlib import animation

LX = 50e-2
LY = 30e-2
T0 = 20.0
T1 = 40.0
T2 = 60.0
HC = 398.0 / (8960.0 * 385.0)
WFRAME = None
DT = 'float32'


def initialize(grid):
    grid.fill(T0)
    grid[:, 0] = T1
    grid[:, -1] = T1
    grid[0] = T1
    grid[-1] = T1 + T2 * \
        vp.sin(vp.pi * vp.linspace(0, LX, grid.shape[1]) / LX)


def compute(grid, coef, temp):
    vp.multiply(grid[1:-1, 1:-1], coef[2], out=temp)
    temp += grid[1:-1, :-2] * coef[0]
    temp += grid[1:-1, 2:] * coef[0]
    temp += grid[2:, 1:-1] * coef[1]
    temp += grid[:-2, 1:-1] * coef[1]
    grid[1:-1, 1:-1] = temp[...]


def heatequation(
        nx,  # The number of grid points in X-direction.
        ny,  # The number of grid points in Y-direction.
        dt,  # The time step interval.
        mt,  # The maximum number of time steps.
        kp,  # The number of time steps for drawing interval.
):
    mx = nx + 2
    my = ny + 2
    grid = vp.empty((my, mx), dtype=DT)
    temp = vp.empty((ny, nx), dtype=DT)

    dx = LX / (nx + 1)
    dy = LY / (ny + 1)

    coef = [
        (HC * dt) / (dx * dx),
        (HC * dt) / (dy * dy),
        1.0 - HC * dt * (2.0 / (dx * dx) + 2.0 / (dy * dy)),
    ]

    x = vp.linspace(0, LX, mx)
    y = vp.linspace(0, LY, my)
    xx, yy = vp.meshgrid(x, y)

    print("initializing grid...", end="", flush=True)
    initialize(grid)
    print("done", flush=True)

    grid_for_plot = [grid, ]
    fig = plt.figure(figsize=(6, 6))
    ax = fig.add_subplot(111, projection='3d')
    print("computing difference method...", end="", flush=True)
    for i in range(int(mt/dt)):
        compute(grid, coef, temp)
        if i % int(kp/dt) == 0:
            grid_for_plot.append(grid.get())
    print("done", flush=True)

    def animate(i):
        global WFRAME
        if WFRAME:
            ax.collections.remove(WFRAME)
        WFRAME = ax.plot_wireframe(
            xx, yy, grid_for_plot[i], rstride=10, cstride=10)
        ax.set_title('time : {:2.1f} [sec]'.format(i * kp))

    def animate_init():
        ax.set_xlabel("x[m]")
        ax.set_ylabel("y[m]")
        ax.set_zlabel("T[$^{\circ}$C]")
        ax.zaxis.set_rotate_label(False)
        ax.set_zlim(T0, T1 + T2)

    print("creating animation...", end="", flush=True)
    animation.FuncAnimation(
        fig,
        animate,
        interval=200,
        frames=int(mt / kp + 1),
        repeat=False,
        init_func=animate_init
    ).save(
        "thermal_simulation.gif",
        writer='pillow'
    )
    print("done", flush=True)


if __name__ == "__main__":
    heatequation(500, 300, 0.001, 30, 1.)

Simulation Result 

../_images/thermal_simulation.gif