サンプル: 流体シミュレーション

目的
物理
プログラム
シミュレーション結果
付録
- 離散方程式

物理 

ナビエ・ストークス方程式 

$\frac{\partial \boldsymbol{u}}{\partial t} + (\boldsymbol{u} \cdot \nabla)\boldsymbol{u} = - \frac{1}{\rho} \nabla p + \frac{\mu}{\rho} \nabla^2 \boldsymbol{u}$

ここで、 $\boldsymbol{u}$ は流速ベクトル場、 $t$ は時間、 $p$ は圧力、 $\rho$ は密度、 $\mu$ は粘度を示します。

シミュレーションの単純化のために、次の無次元方程式を用います。

$\frac{\partial \boldsymbol{u}}{\partial t} + (\boldsymbol{u} \cdot \nabla)\boldsymbol{u} = - \nabla p + \frac{1}{Re} \nabla^{2} \boldsymbol{u}$

$Re$ はレイノルズ数です。

$Re = \frac{\rho V L}{\mu}$

ここで、 $V$ は代表速度、 $L$ は代表長さを示します。

Chorinの射影法 

ナビエ・ストークス方程式を解くために、コリンの射影法 1 2 を用います。方法の詳細については、以下のリストを参照してください。

1: Chorin, A. J. (1967), “The numerical solution of the Navier-Stokes equations for an incompressible fluid”, Bull. Am. Math. Soc. 73: 928–931
2: Chorin, A. J. (1968), “Numerical Solution of the Navier-Stokes Equations”, Math. Comp. 22: 745–762, doi:10.1090/s0025-5718-1968-0242392-2

このサンプルでは、次の計算フローがタイムステップ数だけ繰り返されます。

一時的な流速 $\boldsymbol{u}^{\star}$ を決定します。

$\begin{equation} \boldsymbol{u}^{\star}=\boldsymbol{u}^{n}-\Delta t(\boldsymbol{u}^n \cdot \nabla)\boldsymbol{u}^{n}+\frac{\Delta t}{Re}\nabla^2\boldsymbol{u}^{n} \tag{A} \end{equation}$

ここで、 $\boldsymbol{u}^{n}$ はタイムステップ $n$ での流速です。
ポアソン方程式を解いて圧力 $p^{n+1}$ を決定します。

$\begin{equation} \nabla^2 p^{n+1} = \frac{\nabla \cdot \boldsymbol{u}^{\star}}{\Delta t} \tag{B} \end{equation}$

ポアソン方程式を解くために、ヤコビ法を用います。
流速 $\boldsymbol{u}^{n+1}$ を決定します。

$\begin{equation} \boldsymbol{u}^{n+1} = \boldsymbol{u}^{\star} - \Delta t \nabla p^{n+1} \tag{C} \end{equation}$

境界値条件 

境界値	流速	圧力
流入( $x=0, y=0, y=LY$ )	$0.9, 0.1$	$0$
流出( $x=LX$ )	$\frac{\partial \boldsymbol{u}}{\partial x}=0$	$\frac{\partial p}{\partial x}=0$
物体表面	$(0, 0)$	$\frac{\partial p}{\partial x}=0, \frac{\partial p}{\partial y}=0$
物体内部	$(0, 0)$	$0$

プログラム 

import nlcpy as vp
from matplotlib import pyplot as plt
from matplotlib import animation

Re = 100
DX = .01
DY = .01
DT = .002
NT = 30000
PLOT_INTERVAL = 500
LX = 15.
LY = 10.
NX = int((LX // DX) + 1)
NY = int((LY // DY) + 1)
U_INJ = .9
V_INJ = .1

MAX_ITER_JACOBI = 50
TOL_JACOBI = 1e-3

OBJ_X_BEGIN = int(NX // 4)
OBJ_X_END = int(NX // 4 + NX // 15)
OBJ_Y_BEGIN = int(NY // 2 - NY // 10)
OBJ_Y_END = int(NY // 2 + NY // 10)
OBJ_X_IND = slice(OBJ_X_BEGIN, OBJ_X_END + 1)
OBJ_X_INNER_IND = slice(OBJ_X_BEGIN + 1, OBJ_X_END)  # exclude surface
OBJ_Y_IND = slice(OBJ_Y_BEGIN, OBJ_Y_END + 1)
OBJ_Y_INNER_IND = slice(OBJ_Y_BEGIN + 1, OBJ_Y_END)  # exclude surface

DTYPE = 'float32'


def init():
    u = vp.sca.create_optimized_array((NY, NX), dtype=DTYPE)  # x-axial velocity
    v = vp.sca.create_optimized_array((NY, NX), dtype=DTYPE)  # y-axial velocity
    p = vp.sca.create_optimized_array((NY, NX), dtype=DTYPE)  # pressure
    u_tmp = vp.sca.create_optimized_array((NY, NX), dtype=DTYPE)
    v_tmp = vp.sca.create_optimized_array((NY, NX), dtype=DTYPE)
    p_tmp = vp.sca.create_optimized_array((NY, NX), dtype=DTYPE)
    s = vp.sca.create_optimized_array((NY, NX), dtype=DTYPE)  # right hand side of poisson
    # injection
    u[1:-1, 0] = U_INJ
    v[1:-1, 0] = V_INJ
    u[0, 1:-1] = U_INJ
    v[0, 1:-1] = V_INJ
    u[-1, 1:-1] = U_INJ
    v[-1, 1:-1] = V_INJ
    u_tmp[...] = u
    v_tmp[...] = v
    return u, v, p, u_tmp, v_tmp, p_tmp, s


def bnd_velocity(u, v, u_tmp, v_tmp):
    u[OBJ_Y_IND, OBJ_X_IND] = 0
    v[OBJ_Y_IND, OBJ_X_IND] = 0
    u[1:-1, -1] = u_tmp[1:-1, -2]  # du/dx = 0
    v[1:-1, -1] = v_tmp[1:-1, -2]  # dv/dx = 0


def bnd_pressure(p, p_tmp):
    p[OBJ_Y_INNER_IND, OBJ_X_INNER_IND] = 0
    p[OBJ_Y_IND, OBJ_X_BEGIN] = p_tmp[OBJ_Y_IND, OBJ_X_BEGIN - 1]  # dp/dx = 0
    p[OBJ_Y_IND, OBJ_X_END] = p_tmp[OBJ_Y_IND, OBJ_X_END + 1]      # dp/dx = 0
    p[OBJ_Y_BEGIN, OBJ_X_IND] = p_tmp[OBJ_Y_BEGIN - 1, OBJ_X_IND]  # dp/dy = 0
    p[OBJ_Y_END, OBJ_X_IND] = p_tmp[OBJ_Y_END + 1, OBJ_X_IND]      # dp/dy = 0
    p[1:-1, -1] = p_tmp[1:-1, -2]  # dp/dx = 0


def set_temporary_velocity_kernel(u_w1, v_w1, u_w2, v_w2, c, kernels):
    du_w1, dv_w1, du_w2, dv_w2 = vp.sca.create_descriptor((u_w1, v_w1, u_w2, v_w2))

    desc_u = (
        c[0] * du_w1[0, 0] +
        c[1] * (u_w1[1:-1, 1:-1] * (du_w1[0, 1] - du_w1[0, -1])) +
        c[2] * (v_w1[1:-1, 1:-1] * (du_w1[1, 0] - du_w1[-1, 0])) +
        c[3] * (du_w1[0, 1] + du_w1[0, -1]) +
        c[4] * (du_w1[1, 0] + du_w1[-1, 0])
    )
    kern_u = vp.sca.create_kernel(desc_u, desc_o=du_w2[0, 0])
    kernels['temporary_u'] = kern_u

    desc_v = (
        c[0] * dv_w1[0, 0] +
        c[1] * (u_w1[1:-1, 1:-1] * (dv_w1[0, 1] - dv_w1[0, -1])) +
        c[2] * (v_w1[1:-1, 1:-1] * (dv_w1[1, 0] - dv_w1[-1, 0])) +
        c[3] * (dv_w1[0, 1] + dv_w1[0, -1]) +
        c[4] * (dv_w1[1, 0] + dv_w1[-1, 0])
    )
    kern_v = vp.sca.create_kernel(desc_v, desc_o=dv_w2[0, 0])
    kernels['temporary_v'] = kern_v


def set_poisson_kernel(u, v, p_w1, p_w2, s, c1, c2, kernels):
    du, dv, dp_w1, dp_w2, ds = vp.sca.create_descriptor((u, v, p_w1, p_w2, s))

    desc_right = (
        c1[0] * (du[0, 1] - du[0, -1]) +
        c1[1] * (dv[1, 0] - dv[-1, 0])
    )
    kern_right = vp.sca.create_kernel(desc_right, desc_o=ds[0, 0])
    kernels['poisson_right_hand'] = kern_right

    desc_p = (
        c2[0] * (dp_w1[0, 1] + dp_w1[0, -1]) +
        c2[1] * (dp_w1[1, 0] + dp_w1[-1, 0]) +
        c2[2] * ds[0, 0]
    )
    kern_p = vp.sca.create_kernel(desc_p, desc_o=dp_w2[0, 0])
    kernels['poisson_solve_p'] = kern_p


def set_next_velocity_kernel(u_w1, v_w1, p, u_w2, v_w2, c, kernels):
    du_w1, dv_w1, dp, du_w2, dv_w2 = \
        vp.sca.create_descriptor((u_w1, v_w1, p, u_w2, v_w2))

    desc_u = (
        du_w1[0, 0] + c[0] * (dp[0, 1] - dp[0, -1])
    )
    kern_u = vp.sca.create_kernel(desc_u, desc_o=du_w2[0, 0])
    kernels['next_velocity_u'] = kern_u

    desc_v = (
        dv_w1[0, 0] + c[1] * (dp[1, 0] - dp[-1, 0])
    )
    kern_v = vp.sca.create_kernel(desc_v, desc_o=dv_w2[0, 0])
    kernels['next_velocity_v'] = kern_v


def draw(u, v, ax, ts):
    plt.cla()
    ax.set_title('time : {:.3f}'.format(ts * DT * PLOT_INTERVAL))
    ax.imshow(
        vp.sqrt(u * u + v * v).get(),
        vmin=0, vmax=2.,
        cmap='cividis',
        extent=[0, LX, LY, 0]
    )


def cfd():
    u_w1, v_w1, p_w1, u_w2, v_w2, p_w2, s = init()

    coef1 = [
        1 - (2 * DT / Re) * (1 / (DX * DX) + 1 / (DY * DY)),
        - DT / (2 * DX),
        - DT / (2 * DY),
        DT / (Re * DX * DX),
        DT / (Re * DY * DY)
    ]
    coef2 = [
        1 / (2 * DT * DX),
        1 / (2 * DT * DY)
    ]
    coef3 = [
        DY * DY / (2 * (DX * DX + DY * DY)),
        DX * DX / (2 * (DX * DX + DY * DY)),
        -(DX * DX * DY * DY) / (2 * (DX * DX + DY * DY))
    ]
    coef4 = [
        - DT / (2 * DX),
        - DT / (2 * DY)
    ]

    velocity_kernels = {}
    poisson_kernels = [{}, {}]
    set_temporary_velocity_kernel(u_w1, v_w1, u_w2, v_w2, coef1, velocity_kernels)
    set_poisson_kernel(u_w2, v_w2, p_w1, p_w2, s, coef2, coef3, poisson_kernels[0])
    set_poisson_kernel(u_w2, v_w2, p_w2, p_w1, s, coef2, coef3, poisson_kernels[1])
    set_next_velocity_kernel(u_w2, v_w2, p_w1, u_w1, v_w1, coef4, velocity_kernels)

    fig, ax = plt.subplots()
    u_for_plot = []
    v_for_plot = []
    u_for_plot.append(u_w1.get())
    v_for_plot.append(v_w1.get())
    x, y = vp.linspace(0, LX, NX), vp.linspace(0, LY, NY)
    xx, yy = vp.meshgrid(x, y)

    for ts in range(1, NT + 1):
        # temporary velocity
        u = velocity_kernels['temporary_u'].execute()
        v = velocity_kernels['temporary_v'].execute()
        bnd_velocity(u, v, u_w1, v_w1)
        # poisson
        poisson_kernels[0]['poisson_right_hand'].execute()
        for i in range(MAX_ITER_JACOBI):
            p = poisson_kernels[i % 2]['poisson_solve_p'].execute()
            p_tmp = p_w1 if i % 2 == 0 else p_w2
            bnd_pressure(p, p_tmp)
            err = vp.linalg.norm(p - p_tmp) / vp.linalg.norm(p)
            if err < TOL_JACOBI:
                break
        p_w1[...] = p
        # next velocity
        u = velocity_kernels['next_velocity_u'].execute()
        v = velocity_kernels['next_velocity_v'].execute()
        bnd_velocity(u, v, u_w2, v_w2)
        # keep values for plot
        if ts % PLOT_INTERVAL == 0:
            print(ts)
            u_for_plot.append(u.get())
            v_for_plot.append(v.get())

    def animate(i):
        draw(u_for_plot[i], v_for_plot[i], ax, i)

    def animation_init():
        cs = ax.imshow(vp.sqrt(u*u + v*v), vmin=0, vmax=2., cmap='cividis')
        plt.colorbar(cs, label='Speed', orientation='vertical')
        plt.xlabel("x[m]")
        plt.ylabel("y[m]")

    animation.FuncAnimation(
        fig,
        animate,
        interval=100,
        frames=int(NT / PLOT_INTERVAL + 1),
        repeat=False,
        init_func=animation_init
    ).save(
        "cfd.gif",
        writer='pillow'
    )


if __name__ == '__main__':
    assert OBJ_X_END > OBJ_X_BEGIN
    assert OBJ_Y_END > OBJ_Y_BEGIN
    cfd()

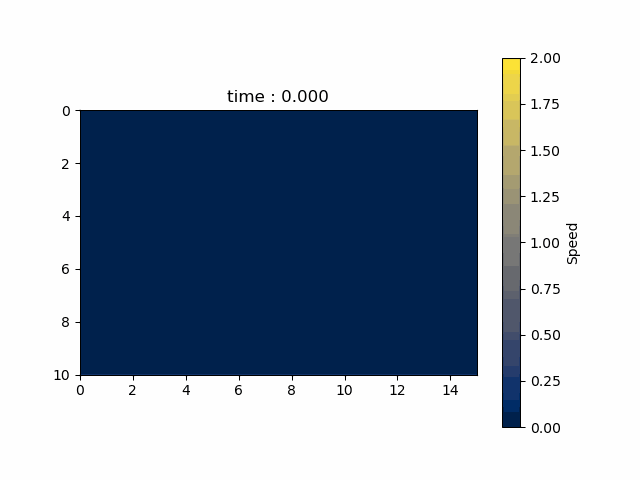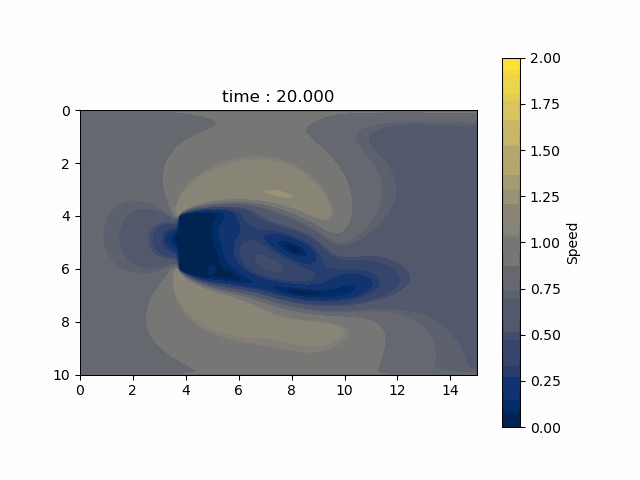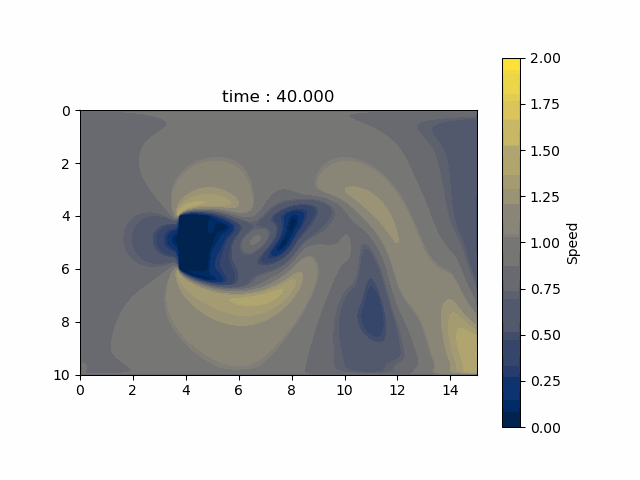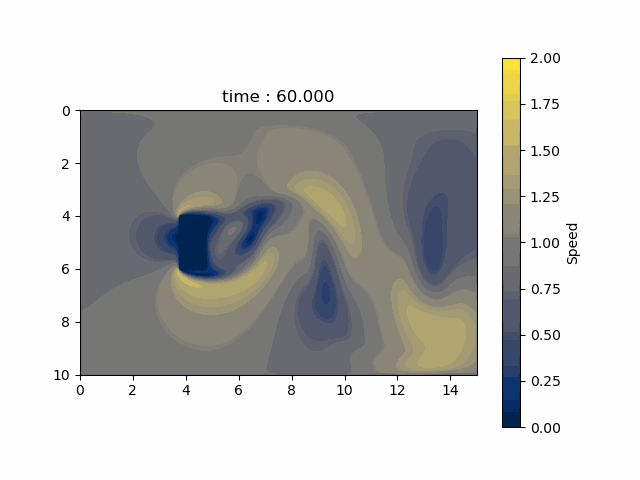
付録 

離散方程式 

上付き文字はタイムステップを示し、下付き文字はx,y座標を示します。

方程式 (A):

$\begin{eqnarray} u^{\star}_{i,j}=(1-\frac{2\Delta t}{Re\Delta x^2}-\frac{2\Delta t}{Re\Delta y^2})u^{n}_{i,j}- \\ \frac{\Delta t}{2\Delta x}u^{n}_{i,j}(u^{n}_{i+1,j}-u^{n}_{i-1,j})- \\ \frac{\Delta t}{2\Delta y}v^{n}_{i,j}(u^{n}_{i,j+1}-u^{n}_{i,j-1})+ \\ \frac{\Delta t}{Re\Delta x^2}(u^{n}_{i+1,j}+u^{n}_{i-1,j})+ \\ \frac{\Delta t}{Re\Delta y^2}(u^{n}_{i,j+1}+u^{n}_{i,j-1}) \end{eqnarray}$

$\begin{eqnarray} v^{\star}_{i,j}=(1-\frac{2\Delta t}{Re\Delta x^2}-\frac{2\Delta t}{Re\Delta y^2})v^{n}_{i,j}- \\ \frac{\Delta t}{2\Delta x}u^{n}_{i,j}(v^{n}_{i+1,j}-v^{n}_{i-1,j})- \\ \frac{\Delta t}{2\Delta y}v^{n}_{i,j}(v^{n}_{i,j+1}-v^{n}_{i,j-1})+ \\ \frac{\Delta t}{Re\Delta x^2}(v^{n}_{i+1,j}+v^{n}_{i-1,j})+ \\ \frac{\Delta t}{Re\Delta y^2}(v^{n}_{i,j+1}+v^{n}_{i,j-1}) \end{eqnarray}$

$u$ 、 $v$ はそれぞれx軸、y軸の流速を示します。

方程式 (B):

$S^{n}_{i,j}=\frac{1}{2\Delta t\Delta x}(u^{\star n}_{i+1,j}-u^{\star n}_{i-1,j})+\frac{1}{2\Delta t \Delta y}(v^{\star n}_{i,j+1}-v^{\star n}_{i,j-1})$

$p^{n+1}_{i,j}=\frac{\Delta y^2(p^{n+1}_{i+1,j}+p^{n+1}_{i-1,j})+\Delta x^2(p^{n+1}_{i,j+1}+p^{n+1}_{i,j-1})-\Delta x^2\Delta y^2 S^{n}_{i,j}}{2(\Delta x^2 + \Delta y^2)}$

ここで、 $S$ はポアソン方程式の右辺を示します。

方程式 (C):

$u^{n+1}_{i,j} = u^{\star}_{i,j}-\frac{\Delta t}{2\Delta x}(p^{n+1}_{i+1,j}-p^{n+1}_{i-1,j})$

$v^{n+1}_{i,j} = v^{\star}_{i,j}-\frac{\Delta t}{2\Delta y}(p^{n+1}_{i,j+1}-p^{n+1}_{i,j-1})$