サンプル: サーマルシミュレーション (SCA実装)

目的
物理
プログラム
シミュレーション結果

目的 

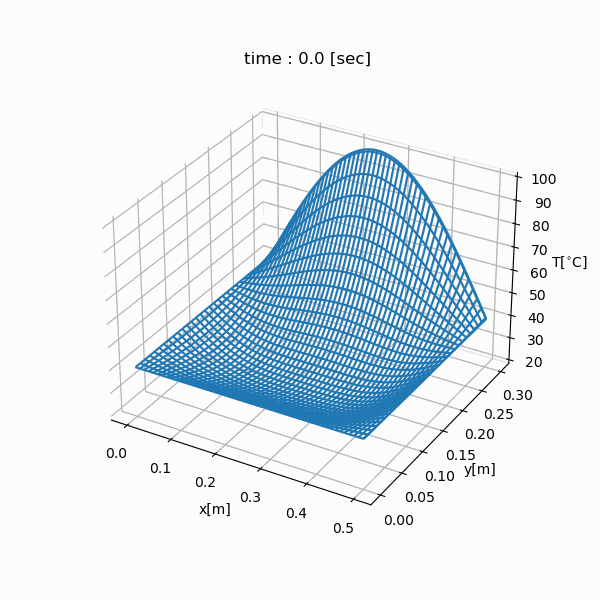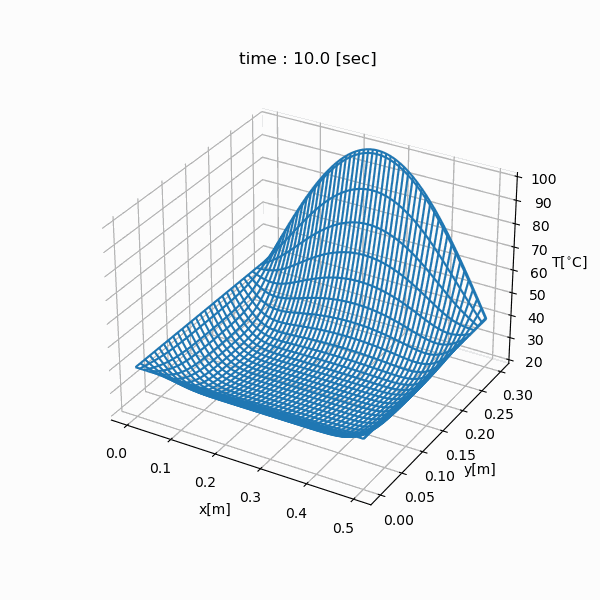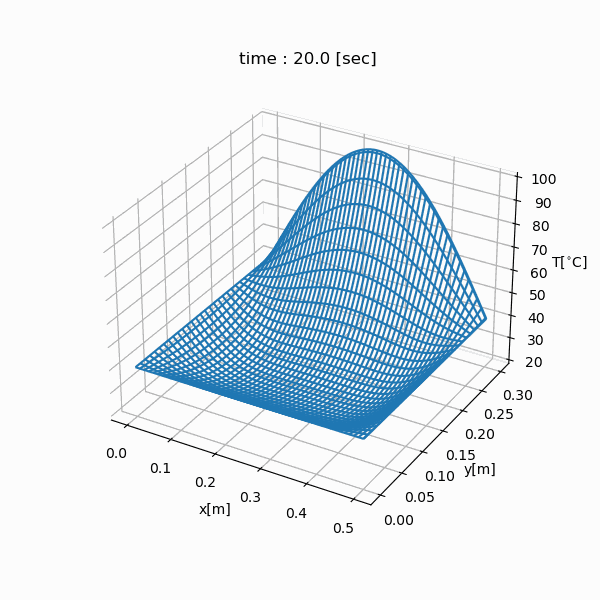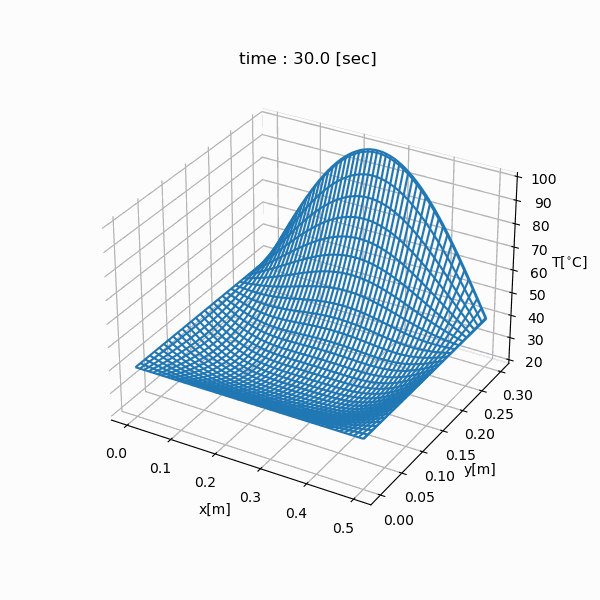
有限差分法を使用して、長さが50 cm（= LX）、幅が30 cm（= LY）の銅の長方形の温度の時間変化をシミュレートします。

物理 

支配方程式 

$\frac{\partial}{\partial t} T=\frac{k}{\rho c}\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right)T$

変数	説明
$T$	温度 [K]
$t$	時間 [s]
$x$	x座標 [m]
$y$	y座標 [m]

定数	説明	銅の値
$k$	熱伝導率	398.0 [W/m K]
$\rho$	密度	8960.0 [kg/m ³]
$c$	比熱容量	385.0 [J/kg K]

境界条件 

$\begin{eqnarray*} T &=& T_1 ~ (x=0, x={\rm LX}, y=0) \\ T &=& T_1+T_2 \sin \frac{\pi x}{\mathrm LX} ~ (y={\rm LY}) \\ \end{eqnarray*}$

初期条件 

$\begin{eqnarray*} T &=& T_0 \\ \end{eqnarray*}$

プログラム 

import nlcpy as vp
from matplotlib import pyplot as plt
from matplotlib import animation

LX = 50e-2
LY = 30e-2
T0 = 20.0
T1 = 40.0
T2 = 60.0
HC = 398.0 / (8960.0 * 385.0)
WFRAME = None
DT = 'float32'


def initialize(grid):
    grid.fill(T0)
    grid[:, 0] = T1
    grid[:, -1] = T1
    grid[0] = T1
    grid[-1] = T1 + T2 * \
        vp.sin(vp.pi * vp.linspace(0, LX, grid.shape[1]) / LX)


def create_stencil_kernel(grid_work1, grid_work2, coef):
    kernels = []
    dgrid1, dgrid2 = vp.sca.create_descriptor((grid_work1, grid_work2))
    # input: grid_work1, output: grid_work2
    desc = ((dgrid1[0, -1] + dgrid1[0, 1]) * coef[0] +
            (dgrid1[-1, 0] + dgrid1[1, 0]) * coef[1] +
            dgrid1[0, 0] * coef[2])
    kernels.append(vp.sca.create_kernel(desc, desc_o=dgrid2[0, 0]))
    # input: grid_work2, output: grid_work1
    desc = ((dgrid2[0, -1] + dgrid2[0, 1]) * coef[0] +
            (dgrid2[-1, 0] + dgrid2[1, 0]) * coef[1] +
            dgrid2[0, 0] * coef[2])
    kernels.append(vp.sca.create_kernel(desc, desc_o=dgrid1[0, 0]))

    return kernels


def heatequation(
        nx,  # The number of grid points in X-direction.
        ny,  # The number of grid points in Y-direction.
        dt,  # The time step interval.
        mt,  # The maximum number of time steps.
        kp,  # The number of time steps for drawing interval.
):
    mx = nx + 2
    my = ny + 2
    grid_work1 = vp.sca.create_optimized_array((my, mx), dtype=DT)
    grid_work2 = vp.sca.create_optimized_array((my, mx), dtype=DT)

    dx = LX / (nx + 1)
    dy = LY / (ny + 1)

    coef = [
        (HC * dt) / (dx * dx),
        (HC * dt) / (dy * dy),
        1.0 - HC * dt * (2.0 / (dx * dx) + 2.0 / (dy * dy)),
    ]

    x = vp.linspace(0, LX, mx)
    y = vp.linspace(0, LY, my)
    xx, yy = vp.meshgrid(x, y)

    print("initializing grid...", end="", flush=True)
    initialize(grid_work1)
    grid_work2[...] = grid_work1
    print("done", flush=True)

    print("creating stencil kernel...", end="", flush=True)
    kernels = create_stencil_kernel(grid_work1, grid_work2, coef)
    print("done", flush=True)

    grid_for_plot = [grid_work1, ]
    fig = plt.figure(figsize=(6, 6))
    ax = fig.add_subplot(111, projection='3d')
    print("computing difference method...", end="", flush=True)
    for i in range(int(mt/dt)):
        grid = kernels[i % 2].execute()
        if i % int(kp/dt) == 0:
            grid_for_plot.append(grid.get())
    print("done", flush=True)

    def animate(i):
        global WFRAME
        if WFRAME:
            ax.collections.remove(WFRAME)
        WFRAME = ax.plot_wireframe(
            xx, yy, grid_for_plot[i], rstride=10, cstride=10)
        ax.set_title('time : {:2.1f} [sec]'.format(i * kp))

    def animate_init():
        ax.set_xlabel("x[m]")
        ax.set_ylabel("y[m]")
        ax.set_zlabel("T[$^{\circ}$C]")
        ax.zaxis.set_rotate_label(False)
        ax.set_zlim(T0, T1 + T2)

    print("creating animation...", end="", flush=True)
    animation.FuncAnimation(
        fig,
        animate,
        interval=200,
        frames=int(mt / kp + 1),
        repeat=False,
        init_func=animate_init
    ).save(
        "thermal_simulation.gif",
        writer='pillow'
    )
    print("done", flush=True)

    for kern in kernels:
        vp.sca.destroy_kernel(kern)


if __name__ == "__main__":
    heatequation(500, 300, 0.001, 30, 1.)

シミュレーション結果 

../_images/thermal_simulation.gif